
開篇引入:在線性回歸模型(一)中的討論中,我們探討了線性回歸模型的基本假設還有相關的推導方法。但是,在線性回歸模型中,是不是每一個變量都對我們的模型有用呢?還是我們需要一個更加優秀的模型呢?下面我們來探討線性回歸的模型選擇吧!
1 子集選擇( )
當我們初步建立的模型中,如果p個預測變量里面存在一些不相關的預測變量,那么我們應該從中間選擇一個比較好的預測變量的子集去重新擬合模型,使我們模型的預測能力 和解釋能力 都能得到提高。
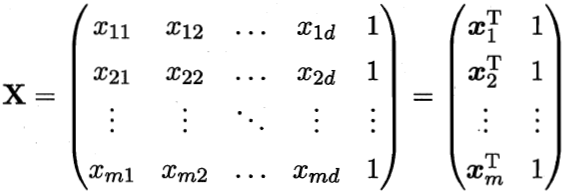
3.1.4 向前逐漸(- )回歸
2壓縮估計( )

通過保留一部分預測變量而丟棄剩余的變量,子集選擇 ( ) 可得到一個可解釋的、預測誤差可能比全模型低的模型.然而,因為這是一個離散的過程(變量不是保留就是丟棄),所以經常表現為高方差,因此不會降低全模型的預測誤差.而壓縮估計 ( ) 更加連續,因此不會受 高易變性 (high ) 太大的影響.

LARS可以作為Lasso的快速求解版本:如果一個非零的系數達到0,則從變量的活躍集中刪除該變量并且重新計算當前的聯合最小二乘方向.

我們來對比下之前學過的子集選擇方法跟我們的壓縮估計在結果上有什么區別:
3降維方法( )
3.3.1 主成分回歸(PCL)
在前面兩節我們討論的都是在原數據上對某些變量集合的子集進行篩選的,主成分分析是一種將原變量做線性組合輸出一系列不相關的其他變量spss主成分回歸步驟,進而使用最小二乘估計。

3.3.2 偏最小二乘回歸(PLS)
由于主成分回歸在降維的過程中只用到了自變量的某些信息,沒有體現自變量與因變量上的某些關系,因此偏最小二乘回歸就是為了解決這個問題。
偏最小二乘法不僅將響應矩陣進行分解提取主因子,也將濃度矩陣進行分解提取主因子。此外spss主成分回歸步驟,在建立校正模型時,不是簡單的將兩個矩陣作主成分分解,而是在將X分解得分矩陣時引入有關Y的得分矩陣的信息,在將Y分解得分矩陣時引入有關X的得分矩陣的信息,這樣可以保證X,Y的得分矩陣之間具有良好的線性關系。
今天的線性回歸模型(二)分享分享到這里啦,接下來的章節中,我們還會給大家介紹如何評價線性回歸模型好壞的殘差分析。大家下期再見!!