
堆排序()是指利用堆積樹(堆)這種數據結構所設計的一種排序算法,它是選擇排序的一種。
算法分析
在學習堆排序之前我們要先了解堆這種數據結構。
堆的定義如下:n個元素的序列{k1,k2,···,kn}當且滿足以下關系時,稱之為堆。
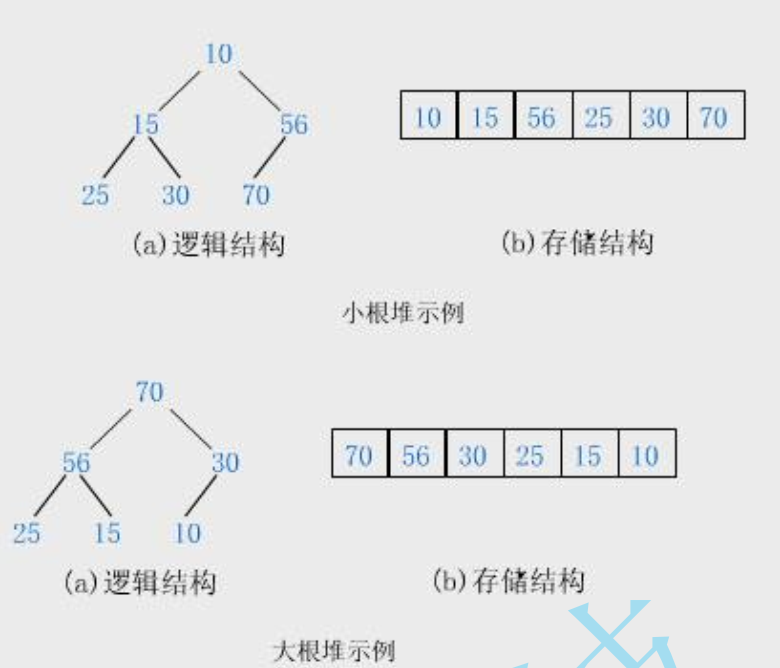
若將此序列所存儲的向量R[1..n]看做是一棵完全二叉樹的存儲結構,則堆實質上是滿足如下性質的完全二叉樹:
樹中任一非葉子結點的關鍵字均不大于(或不小于)其左右孩子(若存在)結點的關鍵字。
對于一個小頂堆,若在輸出堆頂的最小值之后算法分析中實現堆排序c語言程序, 使剩余n-1個元素的序列再次篩選形成一個堆,再輸出次小值,由此反復進行,便能得到一個有序的序列,這個過程就稱之為堆排序。
從上面對于堆排序的敘述我們知道,進行一次堆排序,我們要解決兩個問題:
1、如何初始化一個堆
2、 如何在輸出堆頂元素之后,調整堆內元素,使其再次形成一個堆。

下面我們先來研究第二個問題(為何這樣看了下面的內容你就會明白),以小頂堆為例:
(1)在輸出堆頂元素之后以堆中最后一個元素代替之
。
(2)此時根節點的左右子樹都是堆,由于右子樹根節點的值小于左子樹根節點的值且小于根節點的值,則將9與2互換,互換之后我們發現右子樹的堆結構被破壞了,這時我們將調整后的9作為根節點繼續進行跟上面相同的調整,直到堆結構恢復。
通過上述的調整,我們得到了一個新堆。這也是一次篩選的過程。
其實,初始堆的過程也就是一個反復篩選的過程,若將此序列看成是一個完全二叉樹,則最后一個非終端節點是(N/2)這也是我們篩選的開始點算法分析中實現堆排序c語言程序,從下至上進行篩選過程,最后得到有序序列也就是堆排序。(這一步比較難理解建議自己畫圖看著算法揣摩揣摩)。

代碼實現
#include
#include
void HeapAdjust(int a[],int s,int m)//一次篩選的過程
{
int rc,j;
rc=a[s];
for(j=2*s;j<=m;j=j*2)//通過循環沿較大的孩子結點向下篩選
{
if(ja[j]) break;

a[s]=a[j];s=j;
}
a[s]=rc;//插入
}
void HeapSort(int a[],int n)
{
int temp,i,j;
for(i=n/2;i>0;i--)//通過循環初始化頂堆
{
HeapAdjust(a,i,n);
}

for(i=n;i>0;i--)
{
temp=a[1];
a[1]=a[i];
a[i]=temp;//將堆頂記錄與未排序的最后一個記錄交換
HeapAdjust(a,1,i-1);//重新調整為頂堆
}
}
int main()
{
int n,i;
scanf("%d",&n);
int a[n+1];
for(i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
HeapSort(a,n);
} 復雜度分析
堆排序方法對記錄較少的文件并不值得提倡,但對n較大的文件還是很有效的。
堆排序在最壞情況下,其時間復雜度也為O(nlogn)。