
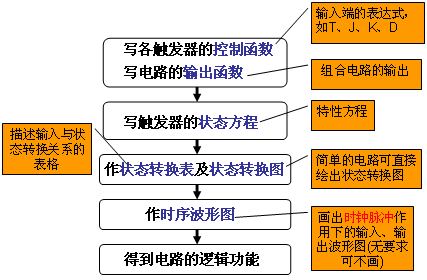
數字邏輯電路種類眾多、千變萬化,但都可以歸結為兩大類:組合邏輯和時序邏輯。一般情況下,組合邏輯用來完成簡單邏輯功能,例如與或非邏輯運算、加法乘法等算術運算。而時序邏輯用來產生與運算過程有關的控制信號序列,例如計數器、分頻電路。它們在數字系統中各自承擔相應的任務。在數字系統中,往往用同步狀態機(同步時序電路)來產生與時鐘周期密切相關的多個控制信號序列,用來控制多路選擇器或數據通道的開啟或關閉,使得組合邏輯運算器能夠有序高效地運行。本文將介紹狀態機及其相關應用。
同步狀態機可以分為兩種:Mealy型、moore型。時序邏輯的輸出取決于現態和輸入,這種稱為Mealy型狀態機。時序邏輯的輸出僅僅取決于現態,而與輸入無關,稱為moore型狀態機。
實例一 串行數據檢測器
設計一個串行數據檢測器,該電路具有一個數據輸入端x和一個輸出端z。當輸入一連串隨機信號時,檢測是否出現序列“1111”,如果有則輸出信號為z=1,對于其他任何輸入序列,輸出都為0。
(1)建立原始狀態圖
分析設計要求,做出合適的狀態圖。在這個檢測過程中,總共可能出現的狀態有5種,分別用S0-S4表示。S0表示起始狀態,表示沒接收到待檢測的序列信號,此時當輸入信號x=0時,次態為S0,輸出信號為z=0,當輸入信號為x=1時,次態變成S1,表示此時已經收到第一個“1”,輸出為z=0。同理,得出各狀態的轉移圖。原始狀態轉移圖
(2)狀態化簡
狀態化簡是指將等價的狀態進行合并,用最少的狀態完成邏輯功能。在保證功能正確的前提下,可以對原始狀態圖進行化簡,刪去多余的狀態數字邏輯電路有什么用,使得系統所需觸發器減少,簡化激勵電路。
如果兩個狀態在相同的輸入條件下,有相同的輸出和相同的次態,則兩個狀態等價數字邏輯電路有什么用,可以合并。因此根據原始狀態圖,可以知道狀態S3和S4等價,可以合并。狀態由5個簡化成4個。
(3)狀態分配。該電路應選用兩級觸發器Q2和Q1,分別用“00”“01”“10”“11”表示s0、s1、s2、s3四種狀態。得到如下狀態表:
狀態轉移表
用卡諾圖進行化簡,得出激勵方程和輸出方程: Q_{2}^{n+1}=xQ_{2}^{n}+xQ_{1}^{n}\\ Q_{1}^{n+1}=xQ_{2}^{n}+x\bar{Q_{1}^{n}}\\ z=xQ_{2}^{n}Q_{1}^{n}
(4)畫出電路圖。在這里可以選用兩個D觸發器來實現邏輯電路。
(5)用實現串行數據檢測器,代碼如下:
module top_module (
input clk,
input reset,
input x,
output z,
output reg [2:0] state);
parameter IDLE=3'b000,A=3'b001,B=3'b010,C=3'b011,D=3'b100;
always@(posedge clk or posedge reset)
if(reset)
state=IDLE;

else
begin
casex(state)
IDLE:if(x==1)
state<=A;
else state<=IDLE;
A:if(x==1)
state<=B;
else state<=IDLE;
B:if(x==1)
state<=C;
else state<=IDLE;
C:if(x==1)begin

state<=D;end
else begin
state<=IDLE;
end
D:if(x==1)begin
state<=D;end
else begin
state<=IDLE;
end
default : state<=IDLE;
endcase
end
assign z =( state == D ) ? 1 : 0 ;
endmodule
測試文件test.v
//測試文件
`timescale 1ns/1ns
`define halfperiod 20
module test;
reg clk,reset;
reg [19:0] data;
wire [2:0] state;
wire z,x;
assign x=data[19];
initial
begin

clk=0;
reset=0;
# 2 reset=1;
# 30 reset=0;
data=20'b1101_0011_1110_1011_0111; //輸入數據流
#(`halfperiod*1000)
$finish;
end
always #(`halfperiod)clk=~clk;
always@(posedge clk)
# 2 data={data[18:0],data[19]};
top_module m(clk,reset,x,z,state);
endmodule仿真后的時序圖如下,檢查輸入輸出關系正確。