
一:
1.優(yōu)先級(jí)隊(duì)列定義:
優(yōu)先級(jí)隊(duì)列( queue) 是0個(gè)或多個(gè)元素的集合,每個(gè)元素都有一個(gè)優(yōu)先權(quán),對(duì)優(yōu)先級(jí)隊(duì)列執(zhí)行的操作有
(1)查找
(2)插入一個(gè)新元素
(3)刪除 一般情況下,查找操作用來(lái)搜索優(yōu)先權(quán)最大的元素,刪除操作用來(lái)刪除該元素 。
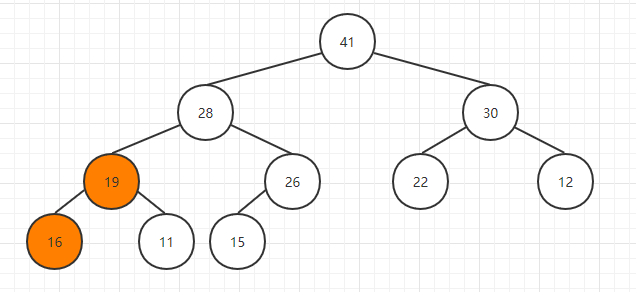
2.最小堆:
最小堆,是一種經(jīng)過(guò)排序的完全二叉樹(shù),其中任一非終端節(jié)點(diǎn)的數(shù)據(jù)值均不大于其左子節(jié)點(diǎn)和右子節(jié)點(diǎn)的值。
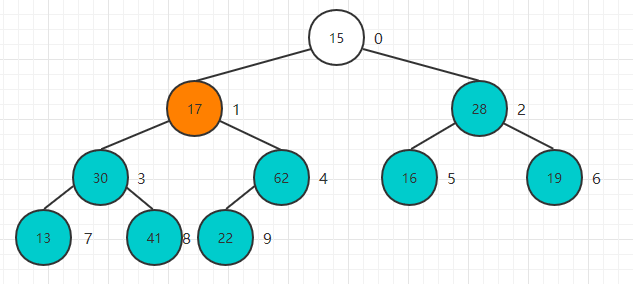
堆存儲(chǔ)在下標(biāo)從0開(kāi)始計(jì)數(shù)的數(shù)組中用堆可以實(shí)現(xiàn)優(yōu)先隊(duì)列,因此,在堆中給定下標(biāo)為i的結(jié)點(diǎn)時(shí):
1 .如果 i = 0,結(jié)點(diǎn) i 是根結(jié)點(diǎn),無(wú)父結(jié)點(diǎn);否則結(jié)點(diǎn) i 的父結(jié)點(diǎn)為結(jié)點(diǎn) [(i - 2) / 2]
2. 如果 2i + 1 > n - 1,則結(jié)點(diǎn) i 無(wú)左子女;否則結(jié)點(diǎn) i 的左子女為結(jié)點(diǎn) 2i + 1
3. 如果 2i + 2 > n - 1,則結(jié)點(diǎn) i 無(wú)右結(jié)點(diǎn);否則結(jié)點(diǎn) i 的右子女為結(jié)點(diǎn) 2i + 2
二:
最小堆的實(shí)現(xiàn):
第一步:利用給定的數(shù)組大小和數(shù)組元素,創(chuàng)建堆空間,并進(jìn)行拷貝。
第二步:調(diào)整成為最小堆
利用自定義的()函數(shù),實(shí)現(xiàn)下滑調(diào)整:
設(shè)置初值指向最后一個(gè)非葉子節(jié)點(diǎn)
1. 從節(jié)點(diǎn)開(kāi)始向下調(diào)整到最后一個(gè)節(jié)點(diǎn)size-1,執(zhí)行 步驟2
2. = -1,如果 >= 0 執(zhí)行步驟1用堆可以實(shí)現(xiàn)優(yōu)先隊(duì)列,(所有的非葉子節(jié)點(diǎn)都遍歷一遍);
template
bool MinHeap::createMinHeap(T *a,int length){
if(length > capacity)
return false;
for(int i = 0; i < length;i++)
heap[i] = a[i];
size = length;
int currentPos = (size-2)/2; //從最后一個(gè)非葉子結(jié)點(diǎn)開(kāi)始向下調(diào)整
while(currentPos >= 0){ //一直到頭節(jié)點(diǎn)
filterdown(currentPos,size-1);
currentPos--;
}
return true;
} 三:
利用最小堆實(shí)現(xiàn)優(yōu)先級(jí)隊(duì)列有兩個(gè)重要的函數(shù):
(int index):對(duì)這個(gè)堆從第index個(gè)結(jié)點(diǎn)向上調(diào)整到頭節(jié)點(diǎn)
template
void MinHeap::filterup(int start){
int j = start;
if(j == 0)
return;
int i = (start-1)/2; //i是start的父親節(jié)點(diǎn)
T temp = heap[start];
while( j > 0){
if(heap[i]>= temp){ //如果父親節(jié)點(diǎn)大于temp
heap[j] = heap[i]; //子節(jié)點(diǎn)就要等于父親節(jié)點(diǎn),父親節(jié)點(diǎn)現(xiàn)在默認(rèn)為temp
j = i; //父親結(jié)點(diǎn)現(xiàn)在是子節(jié)點(diǎn)
i = (i-1)/2; //父親結(jié)點(diǎn)的父親節(jié)點(diǎn)
}else
break; //如果找到一個(gè)父親結(jié)點(diǎn)小于temp,就不需要在向上調(diào)整了,可以保證上邊的節(jié)點(diǎn)都 小于temp
}
heap[j] = temp; //如果向上調(diào)整,找到一個(gè)小于heap[start]的結(jié)點(diǎn),那么調(diào)整就可以結(jié)束了
//結(jié)點(diǎn)j最終等于temp
} (int start,int end) :對(duì)這個(gè)堆從第start個(gè)結(jié)點(diǎn)開(kāi)始向下調(diào)整到end個(gè)結(jié)點(diǎn)
template
void MinHeap::filterdown(int start,int end){
int i = start;
int j = i*2 + 1; //i的左兒子
int temp = heap[i];
if(j > size-1)
return;
while( i <= end){
if(j > size-1)
break;
if(j + 1 <=size-1 && heap[j] > heap[j+1]) //如果右兒子比左兒子小,j表示右兒子
j++; //j表示兩個(gè)兒子中最小的兒子
if(temp < heap[j]) //如果temp比最小的兒子還小,就不需要調(diào)整了
break;
else{ //如果temp比最小的兒子大
heap[i] = heap[j]; //交換i和j ,heap[j]現(xiàn)在默認(rèn)等于temp,所以還沒(méi)有賦值
i = j;

j = 2*i+1;
}
}
heap[i] = temp;
} 四:
最小堆實(shí)現(xiàn)優(yōu)先級(jí)隊(duì)列
插入操作:
1.將size = size + 1
2.將插入的節(jié)點(diǎn)放最小堆的末尾
3.向上調(diào)整到頭節(jié)點(diǎn)
刪除操作:
1.找到刪除節(jié)點(diǎn)的坐標(biāo)
2.將要?jiǎng)h除的節(jié)點(diǎn)與堆最后一個(gè)節(jié)點(diǎn)交換,size = size - 1;
3.從刪除節(jié)點(diǎn)開(kāi)始向下調(diào)整到最后一個(gè)節(jié)點(diǎn)size-1;
完整的程序如下:
#include
#include
using namespace std;
template
class MinHeap{
public:
MinHeap(int cap);
bool insert(T value);
bool remove(T value);
void print();
bool createMinHeap(T *a,int length);
T getTop();
void filterup(int index);
void filterdown(int start,int end);
int size;
private:
int capacity;
T *heap;
};
template
MinHeap::MinHeap(int cap):capacity(cap),size(0),heap(NULL){
heap = new T[capacity];
};
template
T MinHeap::getTop(){
if(size != 0)
return heap[0];
return 0;
}
template
void MinHeap::print(){
for(int i = 0; i < size;i++){
cout<
bool MinHeap::createMinHeap(T *a,int length){
if(length > capacity)
return false;
for(int i = 0; i < length;i++)
heap[i] = a[i];
size = length;
int currentPos = (size-2)/2;
while(currentPos >= 0){
filterdown(currentPos,size-1);
currentPos--;
}
return true;
}
template
void MinHeap::filterup(int start){
int j = start;
if(j == 0)
return;
int i = (start-1)/2;
T temp = heap[start];
while( j > 0){
if(heap[i]>= temp){
heap[j] = heap[i];
j = i;
i = (i-1)/2;
}else
break;
}
heap[j] = temp;
}
template
void MinHeap::filterdown(int start,int end){
int i = start;
int j = i*2 + 1;
int temp = heap[i];
if(j > size-1)
return;
while( i <= end){
if(j > size-1)
break;
if(j + 1 <=size-1 && heap[j] > heap[j+1])
j++;
if(temp < heap[j])
break;
else{
heap[i] = heap[j];
i = j;
j = 2*i+1;

}
}
heap[i] = temp;
}
template
bool MinHeap::remove(T value){ //刪除節(jié)點(diǎn)
bool judge = false;
for(int i = 0; i < size;i++){
if(heap[i] == value){
heap[i] = heap[size-1];
size--;
filterdown(i,size);
judge = true;
}
}
return judge;
}
template
bool MinHeap::insert(T value){ //插入節(jié)點(diǎn)
if(size == capacity){
cout<<"Heap full"<heap(100);
int arr[10] = { 2,1,3,14,7,5,6,9,8,0};
heap.createMinHeap(arr,10);
heap.print();
heap.insert(1);heap.print();
heap.remove(3);heap.print();
}