
以前也零零碎碎發過一些排序算法,但排版都不太好,又重新整理一次,排序算法是數據結構的重要部分,系統地學習很有必要。
時間、空間復雜度比較
1 冒泡排序
算法思想:
比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最后一對。這步做完后,最后的元素會是最大的數。針對所有的元素重復以上的步驟,除了最后一個。持續每次對越來越少的元素重復上面的步驟,直到沒有任何一對數字需要比較。
冒泡排序動圖演示
代碼:
void bubbleSort(int a[], int n)
{
for(int i =0 ; i< n-1; ++i)
{
for(int j = 0; j < n-i-1; ++j)
{
if(a[j] > a[j+1])
{
int tmp = a[j] ; //交換
a[j] = a[j+1] ;
a[j+1] = tmp;
}
}
}
}2 選擇排序
算法思想:
在未排序序列中找到最小(大)元素,存放到排序序列的起始位置從剩余未排序元素中繼續尋找最小(大)元素,然后放到已排序序列的末尾以此類推,直到所有元素均排序完畢
選擇排序動圖演示
代碼:
function selectionSort(arr) {
var len = arr.length;
var minIndex, temp;
for (var i = 0; i < len - 1; i++) {
minIndex = i;
for (var j = i + 1; j < len; j++) {
if (arr[j] < arr[minIndex]) { // 尋找最小的數
minIndex = j; // 將最小數的索引保存
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}3 插入排序
算法思想:
從第一個元素開始,該元素可以認為已經被排序取出下一個元素,在已經排序的元素序列中從后向前掃描如果該元素(已排序)大于新元素,將該元素移到下一位置重復步驟3,直到找到已排序的元素小于或者等于新元素的位置將新元素插入到該位置后重復步驟2~5
插入排序動圖演示

代碼:
void print(int a[], int n ,int i){
cout<4 快速排序
算法思想:
選取第一個數為基準將比基準小的數交換到前面,比基準大的數交換到后面對左右區間重復第二步,直到各區間只有一個數
快速排序動圖演示
代碼:
void QuickSort(vector& v, int low, int high) {
if (low >= high) // 結束標志
return;
int first = low; // 低位下標
int last = high; // 高位下標
int key = v[first]; // 設第一個為基準
while (first < last)
{
// 將比第一個小的移到前面
while (first < last && v[last] >= key)
last--;
if (first < last)

v[first++] = v[last];
// 將比第一個大的移到后面
while (first < last && v[first] <= key)
first++;
if (first < last)
v[last--] = v[first];
}
//
v[first] = key;
// 前半遞歸
QuickSort(v, low, first - 1);
// 后半遞歸
QuickSort(v, first + 1, high);
} 5 堆排序
堆排序()是指利用堆這種數據結構所設計的一種排序算法。堆積是一個近似完全二叉樹的結構,并同時滿足堆積的性質:即子結點的鍵值或索引總是小于(或者大于)它的父節點。
算法思想:
將初始待排序關鍵字序列(R1,R2….Rn)構建成大頂堆,此堆為初始的無序區;將堆頂元素R[1]與最后一個元素R[n]交換,此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2…n-1]tj,tk=1;按增量序列個數k選擇排序法代碼,對序列進行k 趟排序;每趟排序,根據對應的增量ti,將待排序列分割成若干長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因子為1 時選擇排序法代碼,整個序列作為一個表來處理,表長度即為整個序列的長度。
希爾排序動圖演示
代碼:
void shell_sort(T array[], int length) {
int h = 1;
while (h < length / 3) {
h = 3 * h + 1;
}
while (h >= 1) {
for (int i = h; i < length; i++) {
for (int j = i; j >= h && array[j] < array[j - h]; j -= h) {
std::swap(array[j], array[j - h]);
}
}
h = h / 3;
}
}8 計數排序
計數排序統計小于等于該元素值的元素的個數i,于是該元素就放在目標數組的索引i位(i≥0)。
算法思想:
找出待排序的數組中最大和最小的元素;統計數組中每個值為 i 的元素出現的次數,存入數組 C 的第 i 項;對所有的計數累加(從 C 中的第一個元素開始,每一項和前一項相加);向填充目標數組:將每個元素 i 放在新數組的第 C[i] 項,每放一個元素就將 C[i] 減去 1;
計數排序動圖演示
代碼:
#include
#include
#include
using namespace std;
// 計數排序

void CountSort(vector& vecRaw, vector& vecObj)
{
// 確保待排序容器非空
if (vecRaw.size() == 0)
return;
// 使用 vecRaw 的最大值 + 1 作為計數容器 countVec 的大小
int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1;
vector vecCount(vecCountLength, 0);
// 統計每個鍵值出現的次數
for (int i = 0; i < vecRaw.size(); i++)
vecCount[vecRaw[i]]++;
// 后面的鍵值出現的位置為前面所有鍵值出現的次數之和
for (int i = 1; i < vecCountLength; i++)
vecCount[i] += vecCount[i - 1];
// 將鍵值放到目標位置
for (int i = vecRaw.size(); i > 0; i--) // 此處逆序是為了保持相同鍵值的穩定性
vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1];
}
int main()
{
vector vecRaw = { 0,5,7,9,6,3,4,5,2,8,6,9,2,1 };
vector vecObj(vecRaw.size(), 0);
CountSort(vecRaw, vecObj);
for (int i = 0; i < vecObj.size(); ++i)
cout << vecObj[i] << " ";
cout << endl;
return 0;
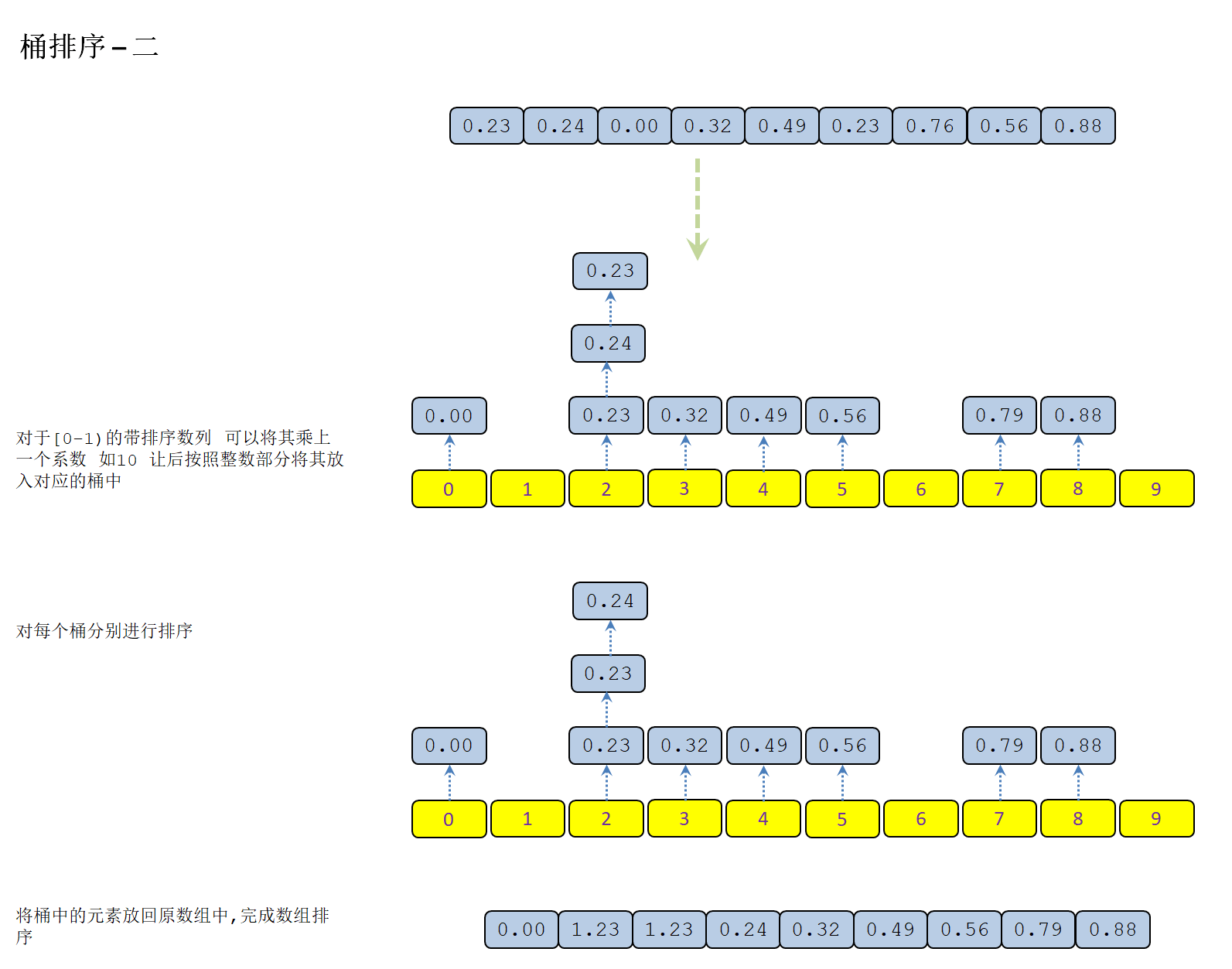
} 9 桶排序
將值為i的元素放入i號桶,最后依次把桶里的元素倒出來。
算法思想:
設置一個定量的數組當作空桶子。尋訪序列,并且把項目一個一個放到對應的桶子去。對每個不是空的桶子進行排序。從不是空的桶子里把項目再放回原來的序列中。
桶排序動圖演示
代碼:
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];

var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; // 輸入數據的最小值
} else if (arr[i] > maxValue) {
maxValue = arr[i]; // 輸入數據的最大值
}
}
// 桶的初始化
var DEFAULT_BUCKET_SIZE = 5; // 設置桶的默認數量為5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets = new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
// 利用映射函數將數據分配到各個桶中
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); // 對每個桶進行排序,這里使用了插入排序
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}10 基數排序
一種多關鍵字的排序算法,可用桶排序實現。
算法思想:
取得數組中的最大數,并取得位數;arr為原始數組,從最低位開始取每個位組成radix數組;對radix進行計數排序(利用計數排序適用于小范圍數的特點)
基數排序動圖演示
代碼:
int maxbit(int data[], int n) //輔助函數,求數據的最大位數
{
int maxData = data[0]; ///< 最大數
/// 先求出最大數,再求其位數,這樣有原先依次每個數判斷其位數,稍微優化點。
for (int i = 1; i < n; ++i)
{
if (maxData < data[i])
maxData = data[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
//p *= 10; // Maybe overflow
maxData /= 10;
++d;
}
return d;
/* int d = 1; //保存最大的位數
int p = 10;
for(int i = 0; i < n; ++i)
{
while(data[i] >= p)
{
p *= 10;
++d;
}
}
return d;*/
}
void radixsort(int data[], int n) //基數排序
{
int d = maxbit(data, n);
int *tmp = new int[n];
int *count = new int[10]; //計數器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //進行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空計數器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //統計每個桶中的記錄數
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //將tmp中的位置依次分配給每個桶
for(j = n - 1; j >= 0; j--) //將所有桶中記錄依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //將臨時數組的內容復制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}
? 2020 GitHub, Inc.