欧美vvv,亚洲第一成人在线,亚洲成人欧美日韩在线观看,日本猛少妇猛色XXXXX猛叫

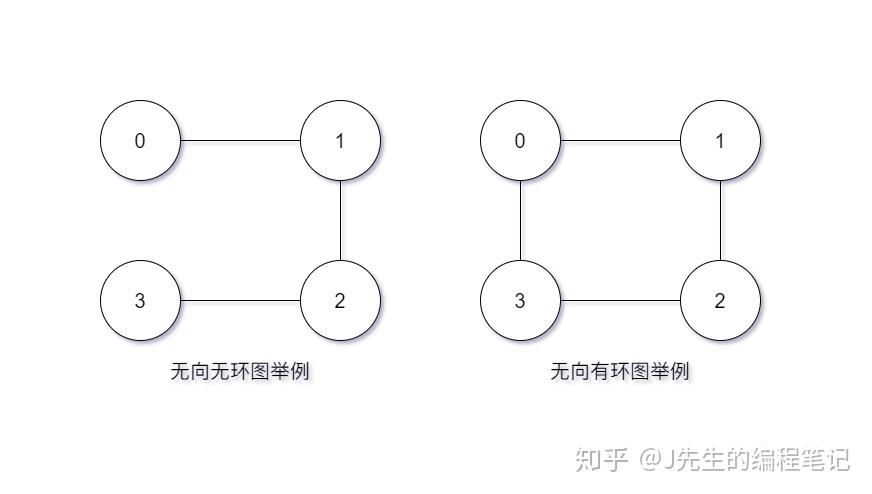
0、什么是環？

在圖論中，環(英語：cycle)是一條只有第一個和最后一個頂點重復的非空路徑。

在有向圖中，一個結點經過兩種路線到達另一個結點，未必形成環。

1、拓撲排序 1.1、無向圖

使用拓撲排序可以判斷一個無向圖中是否存在環，具體步驟如下：

求出圖中所有結點的度。將所有度 ≤ 1 的結點入隊。(獨立結點的度為 0)當隊列不空時拓撲排序判斷是否有環，彈出隊首元素，把與隊首元素相鄰節點的度減一。如果相鄰節點的度變為一，則將相鄰結點入隊。循環結束時判斷已經訪問的結點數是否等于 n。等于 n 說明全部結點都被訪問過，無環；反之，則有環。 1.2、有向圖

使用拓撲排序判斷無向圖和有向圖中是否存在環的區別在于：

2、DFS

使用 DFS 可以判斷一個無向圖和有向中是否存在環。深度優先遍歷圖，如果在遍歷的過程中拓撲排序判斷是否有環，發現某個結點有一條邊指向已訪問過的結點，并且這個已訪問過的結點不是上一步訪問的結點，則表示存在環。

我們不能僅僅使用一個 bool 數組來表示結點是否訪問過。規定每個結點都擁有三種狀態，白、灰、黑。開始時所有結點都是白色，當訪問過某個結點后，該結點變為灰色，當該結點的所有鄰接點都訪問完，該節點變為黑色。

那么我們的算法可以表示為：如果在遍歷的過程中，發現某個結點有一條邊指向灰色節點，并且這個灰色結點不是上一步訪問的結點，那么存在環。

#include?
#include?
#include?
using?namespace?std;

vector>?g;
vector?color;
int?last;
bool?hasCycle;

bool?topo_sort()?{
?int?n?=?g.size();
?vector?degree(n,?0);
?queue?q;
?for?(int?i?=?0;?i???degree[i]?=?g[i].size();
??if?(degree[i]?<=?1)?{
???q.push(i);
??}
?}
?int?cnt?=?0;
?while?(!q.empty())?{
??cnt++;
??int?root?=?q.front();
??q.pop();
??for?(auto?child?:?g[root])?{
???degree[child]--;
???if?(degree[child]?==?1)?{
????q.push(child);
???}
??}
?}
?return?(cnt?!=?n);
}

void?dfs(int?root)?{
?color[root]?=?1;
?for?(auto?child?:?g[root])?{
??if?(color[child]?==?1?&&?child?!=?last)?{
???hasCycle?=?true;
???break;
??}
??else?if?(color[child]?==?0)?{
???last?=?root;
???dfs(child);
??}
?}
?color[root]?=?2;
}

int?main()?{
?int?n?=?4;
?g?=?vector>(n,?vector());

?g[0].push_back(1);
?g[1].push_back(0);
?g[1].push_back(2);
?g[2].push_back(1);
?g[2].push_back(3);
?g[3].push_back(2);
?cout??color?=?vector(n,?0);
?last?=?-1;
?hasCycle?=?false;
?dfs(0);
?cout?
?g[0].push_back(3);
?g[3].push_back(0);
?cout??color?=?vector(n,?0);
?last?=?-1;
?hasCycle?=?false;
?dfs(0);
?cout??return?0;
}

3、Union-Find Set

我們可以使用并查集來判斷一個圖中是否存在環：

對于無向圖來說，在遍歷邊(u-v)時，如果結點 u 和結點 v 的“父親”相同，那么結點 u 和結點 v 在同一個環中。

對于有向圖來說，在遍歷邊(u->v)時，如果結點 u 的“父親”是結點 v，那么結點 u 和結點 v 在同一個環中。

#include?
#include?
#include?
using?namespace?std;

vectorint,?int>>?g;vector?father;int?findFather(int?x)?{int?a?=?x;while?(x?!=?father[x])?{
????????x?=?father[x];
????}while?(a?!=?father[a])?{int?z?=?a;
????????a?=?father[a];
????????father[z]?=?x;
????}return?x;
}void?Union(int?a,?int?b)?{int?fa?=?findFather(a);int?fb?=?findFather(b);
????father[a]?=?father[b]?=?min(fa,?fb);
}bool?isCyclicUnirectedGraph()?{for?(int?i?=?0;?i?????????int?u?=?g[i].first;int?v?=?g[i].second;if?(father[u]?==?father[v])?{return?true;
????????}
????????Union(u,?v);
????}return?false;
}bool?isCyclicDirectedGraph()?{for?(int?i?=?0;?i?????????int?u?=?g[i].first;int?v?=?g[i].second;if?(father[u]?==?v)?{return?true;
????????}
????????father[v]?=?findFather(u);
????}return?false;
}int?main()?{//?Undirected?acyclic?graph//???0//??/?\//?1???2
????g.push_back(make_pair(0,?1));
????g.push_back(make_pair(0,?2));for?(int?i?=?0;?i?3;?i++)?{
????????father.push_back(i);
????}cout?????g.push_back(make_pair(1,?2));vector().swap(father);for?(int?i?=?0;?i?3;?i++)?{
????????father.push_back(i);
????}cout?2vectorint,?int>>().swap(g);
????g.push_back(make_pair(0,?1));
????g.push_back(make_pair(1,?2));
????g.push_back(make_pair(0,?2));vector().swap(father);for?(int?i?=?0;?i?3;?i++)?{
????????father.push_back(i);
????}cout?2
????g.pop_back();
????g.push_back(make_pair(2,?0));vector().swap(father);for?(int?i?=?0;?i?3;?i++)?{
????????father.push_back(i);
????}cout?}

?環 (圖論)?有向無環圖?判斷一個圖是否有環及相關 題目?判斷有向圖是否存在環的 2 種方法(深度遍歷，拓撲排序)