
主成分分析和探索性因子分析是兩種用來探索和簡化多變量復雜關系的常用方法。
主成分分析(PCA)是一種將數據降維技巧,它將大量相關變量轉化成一組很少的不相關變量,這些無相關變量稱為主成分。
探索性因子分析(EFA)是一系列用來發現一組變量的潛在結構的方法。
R基礎安裝包提供了PCA和EFA的函數,分別是()和()。本章重點介紹psych包中提供的函數,該包提供了比基礎函數更豐富和有用的選項。
最常見步驟
1、數據預處理用r軟件做主成分分析,在計算前請確保數據沒有缺失值;
2、選擇因子模型,是選擇PCA還是EFA用r軟件做主成分分析,如果選擇EFA,需要選擇一種估計因子模型,如最大似然法估計;
3、判斷要選擇的主成分/因子數目;

4、選擇主成分/因子;
5、旋轉主成分/因子;
6、解釋結果;
7、計算主成分或因子得分。
主成分分析
加載psych包
()

(psych)
展示基于觀測特征值的碎石檢驗、根據100個隨機數據矩陣推導出來的特征值均值、以及大于1的特征值準則(Y=1的水平線)
fa.([, -1], fa = "pc", n.iter = 100, show. = FALSE, main = 'Scree plot with ')
對數據進行主成分分析
pcpc
加載psych包
()

(psych)
展示基于觀測特征值的碎石檢驗、根據100個隨機數據矩陣推導出來的特征值均值、以及大于1的特征值準則(Y=1的水平線)
fa.(.cor$cov, n.obs=305,fa = "pc", n.iter = 100, show. = FALSE, main = 'Scree plot with ')
對數據.cor進行主成分分析
獲得主成分得分,數據集包含了律師對美國高等法院法官的評分。

()
(psych)
head(pc3$)
獲得律師與法官的接觸頻數與法官評分間的相關系數,執行結果看到兩者關聯非常小。
cor($CONT,pc3$)
獲取主成分得分的系數,.cor數據集包含了305個女孩的8個身體指標
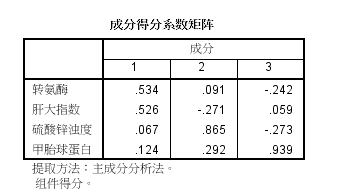
當主成分分析基于相關系數矩陣(如.cor$cov)時,原始數據便不可用了,也不可能獲取每個觀測的主成分得分,但是可以得到用來計算主成分得分的系數。
在身體測量數據中,有各個身體測量指標間的相關系數,但是沒有305個女孩的個體測量值。
()
(psych)
((rc3$),2)
利用如下公式可以得到主成分得分
pc1=0.+0.30arm.span+0.+0..leg-0.-0..-0..girth-0..width
pc2=-0.-0.08arm.span-0.-0..leg+0.+0..+0..girth+0..width