
?作者簡介:熱愛數據處理、數學建模、算法創新的Matlab仿真開發者。
更多Matlab代碼及仿真咨詢內容點擊 :Matlab科研工作室
個人信條:格物致知。
內容介紹
懸臂梁作為一種常見的結構元件,廣泛應用于橋梁、建筑和機械工程等領域。精確計算其模態參數(模態形狀和固有頻率)對于結構動力學分析和設計至關重要。本文將詳細闡述利用Matlab軟件,基于有限元法原理,計算懸臂梁的模態形狀和相應的固有頻率的方法,并對結果進行分析和討論。
一、理論基礎
懸臂梁的振動特性可以用梁的彎曲振動方程描述。對于均勻截面懸臂梁,其無阻尼自由振動方程可表示為:
EI ??w(x,t)/?x? + ρA ?2w(x,t)/?t2 = 0
其中:
該方程的解可以表示為:
w(x,t) = Φ(x)sin(ωt)
其中:
將上述解代入振動方程,可以得到關于模態形狀函數Φ(x)的特征值問題:
EI d?Φ(x)/dx? - ρAω2Φ(x) = 0
邊界條件為:
其中L為梁的長度。求解該特征值問題可以得到梁的固有頻率ω?和相應的模態形狀函數Φ?(x)。
二、有限元法求解
由于解析解僅適用于簡單的邊界條件和梁截面形狀,對于復雜的梁結構,通常采用有限元法進行數值求解。有限元法將連續的梁結構離散成若干個有限單元,通過單元剛度矩陣和質量矩陣的組裝,形成整體結構的剛度矩陣[K]和質量矩陣[M]。然后,求解特征值問題:
[K]{Φ} = ω2[M]{Φ}
其中{Φ}為模態形狀向量。Matlab提供了豐富的線性代數工具,可以高效地求解該特征值問題,得到梁的固有頻率ω?和相應的模態形狀向量{Φ?}。
三、Matlab程序實現
420 * (156);
Me(1, 2) = rho * A * le / 420 * (22 * le);
Me(2, 1) = rho * A * le / 420 * (22 * le);
Me(2, 2) = rho * A * le / 420 * (4 * le^2);
% 組裝整體剛度矩陣和質量矩陣
K(2*i-1:2*i, 2*i-1:2*i) = Ke;
M(2*i-1:2*i, 2*i-1:2*i) = Me;
end
% 應用邊界條件
K(1, :) = 0;
K(:, 1) = 0;
K(1, 1) = 1;
M(1, :) = 0;
M(:, 1) = 0;
% 求解特征值問題
[Phi, Omega] = eig(K, M);
omega = sqrt(diag(Omega));
f = omega / (2 * pi);
% 繪制前五階模態形狀
figure;
for i = 1:5
subplot(5, 1, i);
plot(x, Phi(2:2:end, i));
title(['第', num2str(i), '階模態形狀']);
xlabel('x (m)');
ylabel('w(x)');
end
% 顯示前五階固有頻率
disp(['前五階固有頻率 (Hz): ', num2str(f(1:5)')]);
四、結果分析與討論
上述程序運行后,將得到懸臂梁的前五階固有頻率和相應的模態形狀。模態形狀圖展示了梁在不同頻率下的振動形態,第一階模態形狀對應最低的固有頻率,其振型較為平緩;隨著階數的增加,模態形狀的波峰和波谷數量增多,對應的固有頻率也越高。
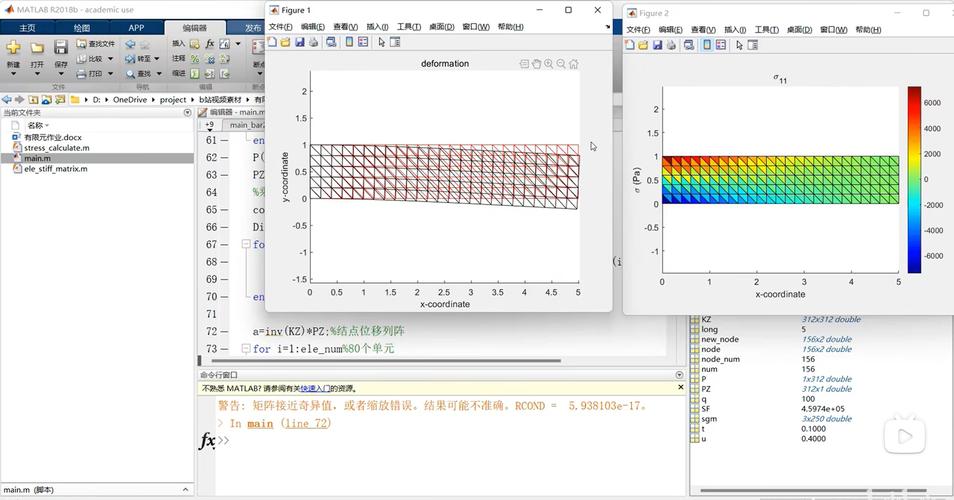
需要注意的是,有限元法的精度與單元個數有關。增加單元個數可以提高計算精度,但同時也增加了計算量。程序中單元個數n的選擇需要根據精度要求和計算資源進行權衡。此外,本程序采用的是簡化的Euler-梁理論,對于厚度較大的梁,需考慮剪切變形的影響,采用梁理論進行分析。
五、結論
本文詳細介紹了利用Matlab基于有限元法計算懸臂梁模態參數的方法,并給出了具體的Matlab程序實現。該方法為工程實際中懸臂梁的動力學分析和設計提供了有效的計算工具。通過調整程序中的參數,可以分析不同材料、截面形狀和長度的懸臂梁的振動特性。 進一步研究可以考慮加入阻尼、非線性因素等,以更準確地模擬實際情況。 同時,可以將該方法擴展到其他類型的梁結構,例如簡支梁、固定端梁等。
?? 運行結果
參考文獻 部分理論引用網絡文獻,若有侵權聯系博主刪除 博客擅長領域: 各類智能優化算法改進及應用 生產調度、經濟調度、裝配線調度、充電優化、車間調度、發車優化、水庫調度、三維裝箱、物流選址、貨位優化、公交排班優化、充電樁布局優化、車間布局優化、集裝箱船配載優化、水泵組合優化、解醫療資源分配優化、設施布局優化、可視域基站和無人機選址優化、背包問題、 風電場布局、時隙分配優化、 最佳分布式發電單元分配、多階段管道維修、 工廠-中心-需求點三級選址問題、 應急生活物質配送中心選址、 基站選址、 道路燈柱布置、 樞紐節點部署、 輸電線路臺風監測裝置、 集裝箱調度、 機組優化、 投資優化組合、云服務器組合優化、 天線線性陣列分布優化、CVRP問題、VRPPD問題、多中心VRP問題、多層網絡的VRP問題、多中心多車型的VRP問題、 動態VRP問題、雙層車輛路徑規劃(2E-VRP)、充電車輛路徑規劃(EVRP)、油電混合車輛路徑規劃、混合流水車間問題、 訂單拆分調度問題、 公交車的調度排班優化問題、航班擺渡車輛調度問題、選址路徑規劃問題、港口調度、港口岸橋調度、停機位分配、機場航班調度、泄漏源定位 機器學習和深度學習時序、回歸、分類、聚類和降維
2.1 bp時序、回歸預測和分類
2.2 ENS聲神經網絡時序、回歸預測和分類
2.3 SVM/CNN-SVM/LSSVM/RVM支持向量機系列時序、回歸預測和分類
2.4 CNN|TCN|GCN卷積神經網絡系列時序、回歸預測和分類
2.5 ELM/KELM/RELM/DELM極限學習機系列時序、回歸預測和分類 2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU門控神經網絡時序、回歸預測和分類
2.7 ELMAN遞歸神經網絡時序、回歸\預測和分類
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/長短記憶神經網絡系列時序、回歸預測和分類
2.9 RBF徑向基神經網絡時序、回歸預測和分類
2。10 DBN深度置信網絡時序、回歸預測和分類 2。11 FNN模糊神經網絡時序、回歸預測 2。12 RF隨機森林時序、回歸預測和分類 2。13 BLS寬度學習時序、回歸預測和分類 2。14 PNN脈沖神經網絡分類 2。15 模糊小波神經網絡預測和分類 2。16 時序、回歸預測和分類 2。17 時序、回歸預測預測和分類 2。18 XGBOOST集成學習時序、回歸預測預測和分類 2。19 各類組合時序、回歸預測預測和分類 方向涵蓋風電預測、光伏預測、電池壽命預測、輻射源識別、交通流預測、負荷預測、股價預測、PM2。5濃度預測、電池健康狀態預測、用電量預測、水體光學參數反演、NLOS信號識別、地鐵停車精準預測、變壓器故障診斷 圖像處理方面 圖像識別、圖像分割、圖像檢測、圖像隱藏、圖像配準、圖像拼接、圖像融合、圖像增強、圖像壓縮感知 路徑規劃方面 旅行商問題(TSP)、車輛路徑問題(VRP、MVRP、CVRP、VRPTW等)、無人機三維路徑規劃、無人機協同、無人機編隊、機器人路徑規劃、柵格地圖路徑規劃、多式聯運運輸問題、 充電車輛路徑規劃(EVRP)、 雙層車輛路徑規劃(2E-VRP)、 油電混合車輛路徑規劃、 船舶航跡規劃、 全路徑規劃規劃、 倉儲巡邏 無人機應用方面 無人機路徑規劃、無人機控制、無人機編隊、無人機協同、無人機任務分配、無人機安全通信軌跡在線優化、車輛協同無人機路徑規劃 通信方面 傳感器部署優化、通信協議優化、路由優化、目標定位優化、Dv-Hop定位優化、Leach協議優化、WSN覆蓋優化、組播優化、RSSI定位優化、水聲通信、通信上傳下載分配 信號處理方面 信號識別、信號加密、信號去噪、信號增強、雷達信號處理、信號水印嵌入提取、肌電信號、腦電信號、信號配時優化、心電信號、DOA估計、編碼譯碼、變分模態分解、管道泄漏、濾波器、數字信號處理+傳輸+分析+去噪、數字信號調制、誤碼率、信號估計、DTMF、信號檢測 電力系統方面 微電網優化、無功優化、配電網重構、儲能配置、有序充電、MPPT優化、家庭用電 元胞自動機方面 交通流 人群疏散 病毒擴散 晶體生長 金屬腐蝕 雷達方面 卡爾曼濾波跟蹤、航跡關聯、航跡融合、SOC估計、陣列優化、NLOS識別 車間調度 零等待流水車間調度問題NWFSP 、 置換流水車間調度問題PFSP、 混合流水車間調度問題HFSP 、零空閑流水車間調度問題NIFSP、分布式置換流水車間調度問題 DPFSP、阻塞流水車間調度問題BFSP